Question

Metallic barium has a body-centered cubic structure (all atoms at the lattice points) and a density of 3.51 g/cm^3. Assume barium atoms to be spheres. The spheres in a body-centered array occupy 68.0% of the total space. Find the atomic radius of barium.

Answer 1

The atomic radius of barium is approximately 0.222 nm.

Molar mass of barium: 137.33 g/mol

Avogadro's constant: 6.02214076 ×
`10^(23) mol^(-1)`

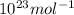
Density of barium: 3.51 g/cm³

First, convert the density to g/cm³:

density = 3.51 g/cm³

Then, calculate the volume per atom:

volume_per_atom = molar_mass / (density * Avogadro's constant)

volume_per_atom = 137.33 g/mol / (3.51 g/cm³ * 6.02214076 ×
`10^(23) mol^(-1)`)

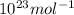volume_per_atom = 5.85 ×
`10^(-23)` cm³

Packing fraction: 0.68

The packing fraction represents the portion of the unit cell occupied by the atoms. We need to find the total volume of the unit cell to calculate the atomic radius.

volume_cell = volume_per_atom / packing_fraction

volume_cell = 5.85 ×
`10^(-23)` cm³ / 0.68

volume_cell = 8.6 ×
`10^(-23)` cm³

Since we know the unit cell is body-centered cubic, we can relate the volume to the edge length (a) using the formula for a cube:

volume_cell =
`a^3`

Taking the cube root of both sides:

a = (volume_cell)^(1/3)

a = (8.6 ×
`10^(-23)` cm³)^(1/3)

a = 0.413 nm

The atomic radius (r) is related to the edge length by the following equation:

r =
`√((3))` a / 4

Plugging in the value of a:

r =
`√((3))` * 0.413 nm / 4

r = 0.222 nm