The area enclosed by the curves
 is approximately 3 square units.
is approximately 3 square units.
To find the area enclosed by , and x=4, we first need to determine the intersection point of the curves
 and
and
 .
.
Setting
 and
and
 equal to each other:
equal to each other:
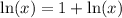
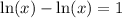
0=1 - This implies there's no intersection.
Therefore, the region enclosed is bounded by
 , and x=4 from x=1 to x=4.
, and x=4 from x=1 to x=4.
Using integration:
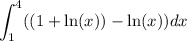
Solving the integral:
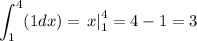
Hence, the area of the enclosed region is 3 square units.
Question:-
Find the area of the indicated region. We suggest you graph the curves to check whether one is above the other or whether they cross, and that you use technology to check your answer. (Round your answer to four decimal places.)
enclosed by y = In(x), y=1In(x), and x = 4