Question

Use a graph to give a rough estimate of the area of the region that lies under the curve y = x./x^(1/2), 0 < x < 4. Then find the exact area.

Answer 1

The exact area of the region beneath the curve y=5sin(x) above the x-axis and on the interval [0,π] is 10.

To estimate the area of the region beneath the curve y=5sin(x) above the x-axis and on the interval [0,π], we can first sketch the graph of the curve.

graph of y = 5sin(x) from 0 to π

From the graph, we can see that the curve is above the x-axis for the entire interval [0,π]. We can also see that the curve oscillates between y=5 and y=−5, so the area of the region beneath the curve is approximately equal to the area of a rectangle with base π and height 10.

Area of rectangle = base * height = π * 10 = 10π

Therefore, our rough estimate of the area of the region is 10π.

To find the exact area of the region, we can use the definite integral formula:

Area =
`\int_a^b f(x) dx`

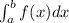
where a and b are the endpoints of the interval and f(x) is the function defining the curve.

In this case, we have a=0, b=π, and f(x)=5sin(x). So, the exact area of the region is given by the following definite integral:

Area =
`\int_0^\pi5 \sin(x) dx`

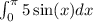
This integral can be evaluated using the following steps:

Integrate 5sin(x) using the formula ∫sin(x)dx=−cos(x)+C,

where C is an arbitrary constant of integration.

Evaluate the integral at the endpoints of the interval and subtract the two values.

The following steps show the detailed solution:

`\int_0^\pi 5 \sin(x) dx` = -5
`\cos(x) \int_0^\pi` =
`(-5 \cos(\pi))` - (-5 \cos(0)) = 10