Question

The length of one leg of a right triangle is 1 cm more than twice the length of the other leg the hypotenuse measures 12 CM find the length of the legs

Answer 1

The lengths of the legs in the right triangle are approximately 5.36 cm and 11.72 cm, where one leg is 1 cm more than twice the length of the other.

Let's denote the lengths of the legs as x and 2x + 1. According to the Pythagorean theorem, the sum of the squares of the two legs is equal to the square of the hypotenuse.

The Pythagorean theorem is given by:

a^2 + b^2 = c^2

where a and b are the legs, and c is the hypotenuse.

In this case:

x^2 + (2x + 1)^2 = 12^2

Now, solve for x:

x^2 + 4x^2 + 4x + 1 = 144

Combine like terms:

5x^2 + 4x + 1 = 144

Subtract 144 from both sides:

5x^2 + 4x - 143 = 0

Factor or use the quadratic formula to find \(x\). In this case, the quadratic formula is:

`\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]`

For the quadratic equation 5x^2 + 4x - 143 = 0, the values are a = 5, b = 4, and c = -143.

After finding x, you can then find the length of the other leg by using 2x + 1.

Solving for
`\(x\) and \(2x + 1\)` will give the lengths of the legs.

Let's use the quadratic formula to find the value of x in the quadratic equation 5x^2 + 4x - 143 = 0:

`\[ x = (-4 \pm √(4^2 - 4(5)(-143)))/(2(5)) \]\[ x = (-4 \pm √(16 + 2860))/(10) \]\[ x = (-4 \pm √(2876))/(10) \]\[ x = (-4 \pm 53.60)/(10) \]`

Now, we have two potential solutions for x:

1.
`\( x = (-4 + 53.60)/(10) \approx 5.36 \)`

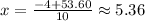
2.
`\( x = (-4 - 53.60)/(10) \approx -5.36 \)` (discard this solution since length cannot be negative)

So,
`\(x \approx 5.36\)`. Now, we can find the length of the other leg:

`\[ 2x + 1 = 2(5.36) + 1 \approx 11.72 \]`

Therefore, the lengths of the legs are approximately
`\(5.36\)` cm and
`\(11.72\)` cm.