Question

Evaluate the given limit​

Answer 1

The limit evaluates to 2, despite the expression being undefined at x=1. This was obtained using L'Hopital's rule.

Evaluating the Limit
`(x^2-1)/(x-1)` as x approaches 1

The expression
`(x^2-1)/(x-1)` is undefined at x=1 due to division by zero. To evaluate the limit as x approaches 1, we need to apply a suitable technique.

*Direct Substitution:*

Directly substituting x=1 in the expression results in the indeterminate form 0/0. This means we cannot directly evaluate the limit using this method.

*L'Hopital's Rule:*

In such cases, L'Hopital's rule comes in handy. This rule states that if the limit of the quotient of two functions f(x) and g(x) as x approaches a is indeterminate, then the limit is equal to the limit of the quotient of their derivatives, provided both derivatives exist and the limit of the second quotient exists.

Formally, if
`lim_(x- > a) f(x)/g(x)` is indeterminate, then:

`lim_(x- > a) f(x)/g(x) = lim_(x- > a) f'(x)/g'(x)`

*Applying L'Hopital's Rule:*

In our case,
`f(x) = x^2 - 1 and g(x) = x - 1.` Differentiating both f and g, we get:

`f'(x) = 2x`

`g'(x) = 1`

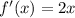
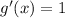
Now, we can apply L'Hopital's rule:

`lim_(x- > 1) (x^2 - 1)/(x - 1) = lim_(x- > 1) (2x)/(1) = 2*1 = 2`

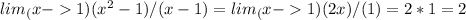
Conclusion:

Therefore, the
`limit of (x^2 - 1)/(x - 1)`as x approaches 1 is 2. This means that as the value of x gets closer and closer to 1, the value of the expression approaches 2.