Question

Can someone please help me on this

Answer 1

The amplitude is half the distance between the midline and the minimum point, which is 8.6 divided by 2. Therefore, the amplitude is 4.3.

to convert a point from polar coordinates
`\((r, \theta)\)` to rectangular coordinates
`\((x, y)\)`, you'll use the following formulas:

`\[x = r \cdot \cos(\theta)\]`

`\[y = r \cdot \sin(\theta)\]`

Given the polar coordinates
`\((r = 2, \theta = (\pi)/(3))\)`:

Substitute the values into the formulas:

`\[x = 2 \cdot \cos\left((\pi)/(3)\right)\]`

`\[y = 2 \cdot \sin\left((\pi)/(3)\right)\]`

Calculate the trigonometric functions:

`\(\cos\left((\pi)/(3)\right) = (1)/(2)\)`

`\(\sin\left((\pi)/(3)\right) = (√(3))/(2)\)`

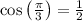
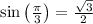
Substitute the trigonometric values into the formulas:

`\[x = 2 \cdot (1)/(2) = 1\]`

`\[y = 2 \cdot (√(3))/(2) = √(3)\]`

Therefore, the rectangular coordinates corresponding to the point given in polar coordinates
`\((2, (\pi)/(3))\)` are
`\((1, √(3))\)` .