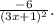The derivative of
 obtained using the quotient rule, where
obtained using the quotient rule, where
 and
and

To find the derivative
 of the given function
of the given function
 you can use the quotient rule. The quotient rule states that if you have a function in the form
you can use the quotient rule. The quotient rule states that if you have a function in the form
 then the derivative is given by:
then the derivative is given by:
![\[ (d)/(dx)\left((u(x))/(v(x))\right) = (u'(x)v(x) - u(x)v'(x))/((v(x))^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zckpzyt1ld4uyfn1ynfjpci9nbz6ust1km.png)
Let's apply this rule to your function:
![\[ u(x) = 2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/af7z1deoagp3hjxav5d83jmbgl913fw4fh.png)
![\[ v(x) = 3x + 1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dazg1kvv4xixe8d4zji3nopj0s4fzllwym.png)
Now, find the derivatives:
![\[ u'(x) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rceruofdj38c3zlk0ub2wslktj1py965oi.png) (since the derivative of a constant is zero)
(since the derivative of a constant is zero)
![\[ v'(x) = 3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/664idk7paeky8w19s60bfvy88o7n6hbplu.png) (the derivative of
(the derivative of
 with respect to
with respect to
 is 3)
is 3)
Now, apply the quotient rule:
![\[ (dy)/(dx) = (u'(x)v(x) - u(x)v'(x))/((v(x))^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/n1wx92sgcmhktbop9jts6mqu09r62da8la.png)
![\[ (dy)/(dx) = (0 \cdot (3x + 1) - 2 \cdot 3)/((3x + 1)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/g5typvfnsdd3cpamcsli93ux2et518g191.png)
Simplify:
![\[ (dy)/(dx) = (-6)/((3x + 1)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/77pq11fsdzxuqlkhwwn51fsmyilecxyi6b.png)
So, the derivative of the given function
 with respect to
with respect to
 is
is