The shaded area below in circle Q, excluding sector RQS, is
 , expressed as a fraction times π. This area is calculated by subtracting the sector area from the total circle area.
, expressed as a fraction times π. This area is calculated by subtracting the sector area from the total circle area.
To find the area shaded below in circle Q, you need to subtract the area of sector RQS from the total area of the circle.
1. Calculate the Total Area of the Circle:
![\[ A_{\text{circle}} = \pi r^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/c3g44fieqantd5sp609tpwctv03gom8qlm.png)
Given that
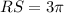 , the radius
, the radius
 .
.
![\[ A_{\text{circle}} = \pi \left((3)/(2)\pi\right)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/wx2379jv45dfxvz5ffu97s78x712vpqvqk.png)
2. Calculate the Area of Sector RQS:
The formula for the area of a sector is
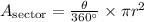 .
.
Since
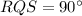 ,
,
![\[ A_{\text{sector}} = (90)/(360) * \pi \left((3)/(2)\pi\right)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/c75aq89vdwasaqv0kqe99nhnp96w20aynv.png)
3. Subtract to Find the Shaded Area:
![\[ \text{Shaded Area} = A_{\text{circle}} - A_{\text{sector}} \]](https://img.qammunity.org/2024/formulas/mathematics/college/hqva3lgd7ygp6kqiptdz80bgf6l3ri9v6c.png)
Perform the calculations to get the shaded area as a fraction times π.
1. Total Area of the Circle:
![\[ A_{\text{circle}} = \pi \left((3)/(2)\pi\right)^2 \] \[ A_{\text{circle}} = (9)/(4) \pi^3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/gvro38uzuannizwwnvi8bbf4pwu5l67sv6.png)
2. Area of Sector RQS:
![\[ A_{\text{sector}} = (90)/(360) * \pi \left((3)/(2)\pi\right)^2 \] \[ A_{\text{sector}} = (1)/(4) \pi^3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/aj8zdfh02ctagx8h6kz0cwy7pxlfstirmd.png)
3. Shaded Area:
![\[ \text{Shaded Area} = A_{\text{circle}} - A_{\text{sector}} \] \[ \text{Shaded Area} = (9)/(4) \pi^3 - (1)/(4) \pi^3 \] \[ \text{Shaded Area} = (8)/(4) \pi^3 \] \[ \text{Shaded Area} = 2 \pi^3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/riii39goz5yf0du7bvz8k0zffzi6ypp7io.png)
Therefore, the shaded area is
 , expressed as a fraction times π.
, expressed as a fraction times π.