Answer:

Explanation:
The point-slope form of a linear equation is given by:
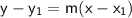
where
 is a point on the line, and
is a point on the line, and
 is the slope.
is the slope.
In this case, the point
 is on the line, and the slope is
is on the line, and the slope is
 .
.
Substitute these values into the point-slope form:
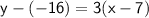

So, the equation of the line in point-slope form is:
