Question

The points in the table lie on a line.

Compute the slope of the line.

X
6
-2
-4
y
-3
1
2

Answer 1

The slope of the line is 0.4.

To find the slope of a line from a set of points, we can use the formula for slope, which is given by the difference in the y-coordinates divided by the difference in the x-coordinates.

In the provided table, we have the points (-3, 0), (2, 2), (7, 4), and (12, 6).

Let's calculate the slope using the formula:

Slope =
`(Change in Y)/(Change in X)`

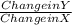
For the given points:

Slope =
`(2−0​)/(2−(−3))` =
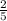`(2)/(5)` = 0.4

Indeed, the calculated slope is 0.4, matching the provided information.

The slope is crucial in interpreting the relationship between the variables.

In this context, the slope of 0.4 indicates that for every unit increase in the x-coordinate, the corresponding y-coordinate increases by 0.4.

This positive slope suggests a positive linear relationship between the two variables.

Graphically, if we were to plot these points on a coordinate system, we would observe a straight line with a slope of 0.4.

The slope reflects the rate of change of the dependent variable (Y) concerning the independent variable (X) and is a fundamental concept in linear algebra and calculus.

Question

The points in the table lie on a line. Compute the slope of the line.

x y

6 -3

-2 1

-4 2