Approximately 5 visitors are expected to buy more than one costume among 400 visitors next week, based on the proportions observed from 232 visitors in the given data.
Let's analyze the information given:
- 206 visitors purchased no costume.
- 23 visitors purchased exactly one costume.
- 3 visitors purchased more than one costume.
The total number of visitors is the sum of these three categories:

Now, if there are 400 visitors expected next week, and the same proportion of visitors purchases more than one costume, you can set up a ratio:
![\[\text{Number of visitors buying more than one costume} : \text{Total number of visitors} = x : 400\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qyihvzyx7dffdw8kmhvytt6prvyecx1z9c.png)
Using the ratio
 (from the given data), you can set up the proportion:
(from the given data), you can set up the proportion:
![\[(3)/(232) = (x)/(400)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jgrhnfk7spmufvuntk4thdt2cz14cqy4yh.png)
Cross-multiply to solve for
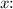
![\[3 * 400 = 232 * x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/p5zxbogev21w9zi767zhcd20wrs4ckg5h3.png)
![\[1200 = 232x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bfb11geev4cdd7t7hlkadyqeftripuqctg.png)
Now, solve for
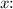
Rounding to the nearest whole number, you would expect about 5 visitors to buy more than one costume.