Question

Consider 8 blood donors chosen randomly from a population. The probability that the donor has type A blood is .40. (a) Find the probability that between 3 and 5 donors (inclusive) will have type A blood (b) Find the probability of 1 or fewer donors having type A blood (c) The probability of 7 or more donors NOT having type A blood is (d)The probability of exactly 5 donors having type A blood is (e) The probability of exactly 5 donors NOT having type A blood is (f) Would it be unusual to see only 1 donor having blood type A?

Answer 1

(a) The probability of 3 to 5 donors having type A blood is 0.63479808.

(b) The probability of 1 or fewer donors having type A blood is 0.10637568.

(c) The probability of 7 or more donors NOT having type A blood is 0.31539456.

(d) The probability of exactly 5 donors having type A blood is 0.12386304.

(e) The probability of exactly 5 donors NOT having type A blood is 0.12386304.

(f) The probability of 1 donor having blood type A is 0.08957952.

(a) Probability of 3 to 5 donors having type A blood:

P(3≤X≤5)=P(X=3)+P(X=4)+P(X=5)

=(
`(8)/(3)` ) .
`0.40^(3)`.
`(1-0.40)^(8-3)` + (
`(8)/(4)` ) .
`0.40^(4)`.
`(1-0.40)^(8-4)` + (
`(8)/(5)` ).
`0.40^(5)` .
`(1-0.40)^(8-5)`

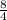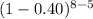
≈ 0.63479808

b) Probability of 1 or fewer donors having type A blood:

P(X≤1)=P(X=0)+P(X=1)

= (
`(8)/(0)`) .
`0.40^(0)` .
`(1-0.40)^(8)`+(
`(8)/(1)`) .
`0.40^(1)` .
`(1-0.40)^(8-1)`

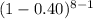
≈0.10637568

(c) Probability of 7 or more donors NOT having type A blood:

P(X≥7)=P(X=7)+P(X=8)

= (
`(8)/(7)` ).
`0.60^(7)`.
`(1-0.40)^(8-7)` + (
`(8)/(8)` ) .
`0.60^(8)`.
`(1-0.40)^(8-8)`

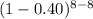
≈0.31539456

(d) Probability of exactly 5 donors having type A blood:

P(X=5)=(
`(8)/(5)`).
`0.40^(5)`.
`(1-0.40)^(8-5)`

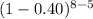
≈0.12386304

(e) Probability of exactly 5 donors NOT having type A blood

P(X=3) = (
`(8)/(3)` ) .
`0.60^(3)` .
`(1-0.40)^(8-3)`

≈0.12386304

(f) Probability of 1 donor having blood type A

P(X=1) = (
`(8)/(1)` ) .
`0.40^(1)`.
`(1-0.40)^(8-1)`

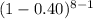
≈0.08957952