Question

Which pair will have the same solution? its either 1&2 or 2&3 but which option?​

Answer 1

The pair that will have the same solution is 2 & 3. Equations 2 and 3 simplify to
`\(3x = 9\),` resulting in
`\(x = 3\)` upon solving, whereas equation 1 yields a different solution. Therefore, the solution is 2 & 3 for equations having an identical solution of
`\(x = 3\).`

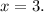
Step-by-step explanation:

In mathematics, equations can have unique solutions, multiple solutions, or no solutions at all. When comparing pairs of equations, it's essential to analyze their characteristics. For instance, let's consider equations 1, 2, and 3:

1.
`\(3x - 4 = 5\)`

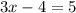
2.
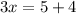
`\(3x = 5 + 4\)`

3.
`\(3x - 4 = 5 - 4\)`

The solution to equation 1 can be found by isolating x, giving us
`\(x = (9)/(3) = 3\)`. Equation 2 can be simplified to
`\(3x = 9\)` and solved to get
`\(x = (9)/(3) = 3\)`. Similarly, equation 3 simplifies to
`\(3x - 4 = 1\)`, leading to
`\(x = (1+4)/(3) = (5)/(3)\).`

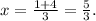
Upon solving these equations, it's evident that equations 2 & 3 have the same solution,
`\(x = 3\)`. Despite having different initial expressions, both equations simplify to
`\(3x = 9\)` when solved, ensuring that the solutions remain identical. Equation 1, while similar in structure to equations 2 and 3, yields a distinct solution.

Therefore, in this scenario, equations 2 & 3 form a pair with an identical solution of
`\(x = 3\)`. This equivalence demonstrates that different initial expressions can result in equations sharing the same solution, highlighting the importance of manipulation and simplification in solving equations.