Question

Question 6

Priya is using the quadratic formula to solve two different quadrat
For the first equation, she writes x =
For the second equation, she writes x =
4+√16-72
12
8+√64-24
6
Edit View Insert Format Tools Table
| BIU
Which equation(s) will have real solutions? Which equation(s) will
12pt Paragraph
.
A
✓ T²V || D

Answer 1

The equation with a positive discriminant
`(\(b^2 - 4ac\))` has real solutions. In the given options, the second equation
`(\(8 + √(64 - 24)/6\))` will have real solutions.

It seems like part of the information in your question is missing. The quadratic formula to find the solutions for a quadratic equation
`\(ax^2 + bx + c = 0\)` is given by:

`\[ x = (-b \pm √(b^2-4ac))/(2a) \]`

For the solutions to be real, the expression under the square root
`(\(b^2 - 4ac\))`, known as the discriminant, must be greater than or equal to zero.

Let's apply this to the equations mentioned:

1. First equation:
`\( x = (4 + √(16 - 72))/(12) \)`

2. Second equation:
`\( x = (8 + √(64 - 24))/(6) \)`

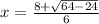
Now, let's evaluate the discriminant for each equation:

1. First equation:
`\( 16 - 72 = -56 \)` (negative discriminant)

2. Second equation:
`\( 64 - 24 = 40 \)` (positive discriminant)

For real solutions, the discriminant must be greater than or equal to zero. Therefore, the second equation will have real solutions, while the first equation will not.

In conclusion:

- The second equation will have real solutions.

- The first equation will not have real solutions.