Shade the region to the left of -2 (including -2) on a number line is p ≤ -2.
Part A:
To solve the inequality $\dfrac{4}{5}-\dfrac12p \ge \dfrac95$, we manipulate it step-by-step as follows:
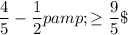
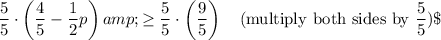
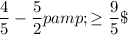
10
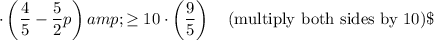

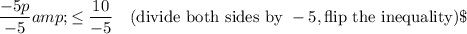

Therefore, the solution to the inequality is
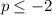 .
.
Part B:
To graph the solution
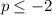 on a number line, first draw a number line and mark a point at -2. Shade the region to the left of -2 (including -2 itself) since all values of p that are less than or equal to -2 satisfy the inequality.
on a number line, first draw a number line and mark a point at -2. Shade the region to the left of -2 (including -2 itself) since all values of p that are less than or equal to -2 satisfy the inequality.
Here's how the graph would look like:
|-------|-------|-------|-------|-------|-------|
-5 -4 -3 -2 -1 0