Question

The parent function f(x)=x³ is represented by graph A. Graph A is transformed to get graph B and Graph C. Write the functions represented by graph B and graph C. Write the functions represented by graph B and graph C.

Answer 1

Graph B represents the function
`\(g(x) = (x - a)^3 + b\)`, and Graph C represents the function
`\(h(x) = - (x - c)^3 + d\)`, where a, b, c, and d are constants that determine the specific transformations applied to the parent function
`\(f(x) = x^3\).`

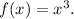
Step-by-step explanation:

The function
`\(f(x) = x^3\)` is the parent function, and Graph A represents this cubic function without any transformations. To obtain Graph B, we apply a horizontal translation to the right by a units and a vertical translation upward by b units. The general form for this transformation is g(x) = (x - a)³ + b\), where a controls the horizontal shift, and b controls the vertical shift.

For Graph C, we apply a horizontal translation to the left by c units and a vertical reflection (flipping upside down) followed by a vertical translation downward by d units. The general form for this transformation is h(x) = - (x - c)³ + d, where c determines the horizontal shift, and d determines the vertical shift.

In summary, when dealing with cubic functions, horizontal shifts are determined by values inside the parentheses, and vertical shifts are determined by values outside the parentheses. The signs of these values and their magnitudes determine the direction and distance of the shifts, respectively. Therefore, the transformations described by a, b, c, and d dictate the specific changes applied to the parent cubic function to produce Graphs B and C.