Question

What is the ratio of the volume of the gray sphere to the volume of the orange sphere?

Answer 1

Volume of the orange sphere, in a ratio of 8:27 to the gray sphere (144π), is 486π cubic units.

Given the ratio of volumes for the gray and orange spheres is 8:27 and the volume of the gray sphere is 144π cubic units, we can determine the volume of the orange sphere.

Let's denote the volume of the orange sphere as
`\(V_o\)`.

The ratio of the volumes is 8:27, implying that the ratio of the gray sphere's volume to the orange sphere's volume is 8:27.

So, setting up a proportion using the given volumes:

`\(\frac{{\text{Volume of Gray Sphere}}}{{\text{Volume of Orange Sphere}}} = \frac{{144\pi}}{{V_o}}\)`

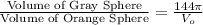
Using the ratio 8:27,

`\((144\pi)/(V_o) = (8)/(27)\)`

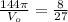
Cross-multiplying:

`\(8V_o = 27 * 144\pi\)\(V_o = (27 * 144\pi)/(8)\)\(V_o = (3888\pi)/(8)\)\(V_o = 486\pi\)`

Therefore, the volume of the orange sphere is \(486\pi\) cubic units, considering the ratio of volumes between the gray and orange spheres and the given volume of the gray sphere as 144π cubic units.

Question:

Two spheres, one gray and one orange, have volumes in a ratio of 8:27. If the gray sphere's volume is 144π cubic units, what is the volume of the orange sphere?