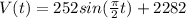Question

In a normal respiratory cycle the volume of air that moves into and out of the lungs is about 504 mL. The reserve and residual volumes of air that remain in the lungs occupy about 2030 mL and a single respiratory cycle for an average human takes about 4 seconds. Find a model for the total volume of air V(t) in the lungs as a function of time.

Answer 1

`V(t)=252sin((\pi)/(2)t )+2282`

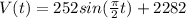
Step-by-step explanation:

The volume of air increases and decreases, hence the volume of air can be represented as a sine function.

A sine function is of the form:

y = Asin(B(x - C)) + D

Where A is the amplitude, B is the frequency, C is the horizontal shift and D is the vertical shift.

Therefore, the total volume of air V(t) in the lungs as a function of time is given by:

V(t) = Asin(B(t - C)) + D

Since the volume of air in and out of the longs is 504 ml, hence the amplitude (A) = 504/2 = 252

There is residual air of 2030 ml minimum in the lungs and a maximum of 2534 ml (2030 ml + 504 ml), hence the vertical shift (D) = (2534 + 2030) / 2 = 2282 ml

The frequency B = 2π / 4 s = π/2

Therefore:

`V(t)=252sin((\pi)/(2)t )+2282`