Answer:
a) See attached (sorry if its a bit unneat, use 5 points for more accuracy while drawing. 3 points is generally accepted though.)
b) 80 mins
c) 4000 meters, 40 minutes
Explanation:
First, lets define the literal meaning of the questions.
A) Graph the function (I will explain how to do below)
B) What is the absolute value of the distance of the x-intercepts?
C) What is the y value of the vertex (maximum/ minimum value). What is the x value of the vertex?
Lets solve these problems. To graph a quadratic equation by hand, first you must find the vertex. Formula for the x-value of the vertex:

Because a quadratic equation is in the form:
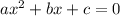
We can find the values of a and b.
Values of a and b in this equation:
a: -2.5
b: 200
Plug into the vertex formula (shown above), -b/2a
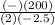
Simplify.

Simplify.
-200/-5 = 40
Now we have 40, the x value of the vertex. Plug 40 back into the x values of the problem (t in this word problem) to find the y value of the vertex.
The equation:
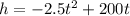
Plug in 40 to the t values.
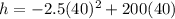
Simplify.
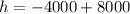
Add.
h = 4000
Now, we have the values of the vertex.
Values of vertex:
x: 40
y: 4000
This means that when the x-value is 40, the y-value is 4000. In this case, it means 40 minutes in, the altitude of the plane is 4000 meters.
On a graph, draw a point at x-value 40 and y-value 4000. This will be needed when we draw the graph.
We need at least 3 points to graph a quadratic equation (this applies to all parabolas.)
This part is a bit hard to explain, but you will get it with this example. Since we need 3 points, we need to solve for 2 more points like we just did. But what x-values do we use? For the vertex, we knew the x value was -b/2a!
Solve for x-values that have an equivalent absolute distance from the x value of the vertex.
For example, in this case, the x value of the vertex is 40.
If we were to pick the x value of 38 for the 2nd point, we would have to use the 42 for the 3rd point as they are both 2 away from 40.
|40-38| = 2
|40-42| = 2
I will use the x values of 38 and 42 to graph this. Lets do the same thing we did to find the y value of the vertex. Plug the x values into the equation individually.
Equation:
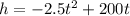
Plug in 38 to the x values (in this case its called t.)
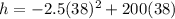
Simplify.
h = -3610 + 7600
Add.
h = 3990
This means when the x value of the parabola is 38, the y value is 3990. In this case, it means after the plane has flown for 38 minutes, the altitude of the plane is 3990.
Now lets find what the y-value of the parabola would be when the x-value is 42 (when we've did this, we can graph it.)
But here is a little trick to speeden things up. If the absolute value of the difference of the x-value of the vertex (40 in this case) and the x value of the point we just found (38 in this case) is the same as the absolute value of the difference of the 3rd point we need to graph (42 in this case), which is always true if you followed the steps above, the y value is the same!
So, this means, when:
Point 2:
x: 38
y: 3990
Point 3:
x: 42
y: 3990
The y-value of the 3rd point we need to find is 3990.
Now we can graph it using our points.
Point 1 (Vertex):
x: 40
y: 4000
Point 2:
x: 38
y: 3990
Point 3:
x: 42
y: 3990
I'll just use paint to draw this, draw the points, label them, and connect the points with a parabola.
Now lets answer b using the definitions.
Because we need to find the x intercepts, lets use the quadratic formula.
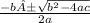
Ignore the A's, its a bug.
If you need to know how to use the quadratic equation, DM me. Otherwise, I will just write the x-intercepts.
x-intercepts:
0,80
Because it is asking for the distance between Toronto and Montreal in minutes, subtract 0 from 80.
80-0=80
B) 80 minutes
The maximum height of the aircraft is the y value of the vertex and the time that the aircraft reaches this height is the x-value of the intercept.
(Vertex):
x: 40
y: 4000
C) 4000 meters, 40 minutes