Question

Answer questions below please I really need help

Answer 1

A. After 12 years, the average cost of college is estimated to be approximately $67,455.83 per year, given an annual increase of 8.2%. B. To cover 1 year of college in 12 years, invest approximately $14,711.94 now at a 5.5% continuous compound interest rate.

Let's solve each part of the problem step by step:

(a) Average Cost Increase:

- The formula for compound interest is
`\(A = P(1 + r/n)^(nt)\)`, where:

- A is the future value,

- P is the principal (initial amount),

- r is the annual interest rate (in decimal form),

- n is the number of times interest is compounded per year,

- t is the number of years.

- For this problem, P is the current average cost, r is the annual increase rate, and t is the number of years.

- The future average cost after 12 years is
`\(A = 30,639 * (1 + 0.082)^(12)\)`.

(b) Savings Plan:

- For continuous compounding, the formula is
`\(A = Pe^(rt)\)`, where:

- A is the future value,

- P is the principal,

- e is the mathematical constant approximately equal to 2.71828,

- r is the interest rate,

- t is the time in years.

- Rearrange the formula to find \(P = \frac{A}{e^{rt}}\).

- The amount needed in the savings plan now is
`\(P = (30,639)/(e^(0.055 * 12))\)`.

Let's calculate the final answers:

(a) Average Cost Increase:

-
`\(A = 30,639 * (1 + 0.082)^(12) \approx 67,455.83\)`

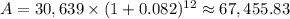
(b) Savings Plan:

-
`\(P = (30,639)/(e^(0.055 * 12)) \approx 14711.94\)`

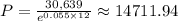
After 12 years, the average cost of college will be approximately $67,455.83 per year. To pay for 1 year of college 12 years from now, you should put approximately $14,711.94 in the savings plan now.