Question

Wally Brown is planning for his retirement, so he is setting up a payout annuity with his bank. For twenty-five years, he wishes to receive annual payouts that start at $13,000 and then receive an annual COLA of 3.5%. (Round your answers to the nearest cent.)

(a) How much must he deposit if his money earns 8.3% interest per year? $
(b) How large will Wally's first annual payout be? $
(c) How large will Wally's second annual payout be? $
(d) How large will Wally's last annual payout be? $

Answer 1

(a) Wally must deposit approximately $136,032.53.

(b) Wally's first annual payout will be approximately $13,000.

(c) Wally's second annual payout will be approximately $13,455.00.

(d) Wally's last annual payout will be approximately $37,495.27.

Step-by-step explanation:

(a) Wally's initial deposit (P) can be calculated using the present value formula for an annuity:

`\[ P = PMT * \left( (1 - (1 + r)^(-n))/(r) \right) \]`

where PMT is the annual payment, r is the interest rate per period, and n is the total number of periods. Plugging in the values, we get:

`\[ P = 13000 * \left( (1 - (1 + 0.083)^(-25))/(0.083) \right) \]`

`\[ P \approx 136032.53 \]`

(b) For the first annual payout, Wally receives the fixed amount of $13,000.

(c) For subsequent years, the payout is adjusted for inflation using the cost-of-living adjustment (COLA) formula:

`\[ P_t = P_(t-1) * (1 + \text{COLA}) \]`

where
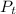`\(P_t\)` is the payout in year t and COLA is the cost-of-living adjustment rate. For Wally's second payout:

`\[ P_2 = 13000 * (1 + 0.035) \]`

`\[ P_2 \approx 13455.00 \]`

(d) For the last payout, the calculation is similar:

`\[ P_(25) = 13000 * (1 + 0.035)^(24) \]`

`\[ P_(25) \approx 37495.27 \]`

These calculations ensure that Wally's annual payouts are adjusted for inflation while considering the interest earned on his initial deposit.