Question

Triangle XYZ has an altitude as shown. Eric and Maggie are both trying to prove the law of sines. A diagram of a triangle XYZ. Two perpendicular lines are drawn from the vertex Y to XZ and from the vertex Z to XY. The length of XY is z, XZ is y, YZ is x, and the height of the perpendicular lines is h1 and h2. Eric's Work Maggie's Work sin ⁡ ( X ) = h 1 z and sin ⁡ ( Z ) = h 1 x h 1 = z ⁢ sin ⁡ ( X ) and h 1 = x ⁢ sin ⁡ ( Z ) sin ⁡ ( Y ) = h 2 x and sin ⁡ ( X ) = h 2 y h 2 = x ⁢ sin ⁡ ( Y ) and h 2 = y ⁢ sin ⁡ ( X ) The proof was correctly started by . The next step in the proof is to by the .

Answer 1

Both Eric and Maggie correctly start by expressing heights
`\(h_1\)` and
`\(h_2\)` in terms of sides and angles using sine. The next step is equating

`\(z \sin(X)\) and \(x \sin(Y)\)`.

Eric's Work:

1. Eric starts with the definition of sine:
`\( \sin(X) = (h_1)/(z) \)`, where
`\(h_1\)` is the height of the perpendicular from Y to XZ.

2. He rearranges the equation to solve for
`\(h_1\): \( h_1 = z \cdot \sin(X) \).`

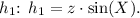
Maggie's Work:

1. Maggie also begins with the definition of sine:
`\( \sin(Y) = (h_2)/(x) \)`, where
`\(h_2\)` is the height of the perpendicular from Z to XY.

2. Similar to Eric, she rearranges the equation to solve for
`\(h_2\): \( h_2 = x \cdot \sin(Y) \).`

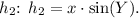
Both Eric and Maggie have correctly started their proofs by expressing the heights
`\(h_1\)` and
`\(h_2\)` in terms of the sides and angles using the sine function.

Next Steps:

The next step in the proof is to set these two expressions for \(h_1\) and
`\(h_2\)` equal to each other. This can be done by equating the right-hand sides of Eric and Maggie's equations:

`\[ z \cdot \sin(X) = x \cdot \sin(Y) \]`

This establishes the relationship between the sides and angles of the triangle, which is a key step in proving the law of sines. The next steps might involve simplifying the equation further and generalizing it to arrive at the more familiar form of the law of sines.