Question

Robert’s uncle owns a 510-acre farm. He grows only squash and pumpkins on his farm. This year he wants to plant 190 more acres of pumpkins than acres of squash. How many acres of pumpkins does Robert’s uncle need to plant?

Answer 1

Answer: 350

Explanation:

Pumpkin area (P) = Squash area (S) + 190 acres

Total farm area = Squash area + Pumpkin area

Total farm area = 510 acres

We can express this mathematically:

[ S + P = 510 ] [ P = S + 190 ]

Substitute the second equation into the first:

[ S + (S + 190) = 510 ] [ 2S + 190 = 510 ] [ 2S = 320 ] [ S = 160 ]

Now let’s find the pumpkin area:

[ P = S + 190 ] [ P = 160 + 190 ] [ P = 350 ]

Robert’s uncle needs to plant 350 acres of pumpkins.

Answer 2

Robert's uncle needs 350 acres of pumpkins.

Explanation:

Let's denote the number of acres of squash as
`\sf S` and the number of acres of pumpkins as
`\sf P`.

The problem states that the uncle wants to plant 190 more acres of pumpkins than acres of squash. This can be expressed as an equation:

`\sf P = S + 190`

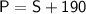
The total number of acres on the farm is 510 acres, so the sum of the acres of squash and pumpkins must equal 510:

`\sf S + P = 510`

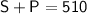
Now, substitute the expression for
`\sf P` from the first equation into the second equation:

`\sf S + (S + 190) = 510`

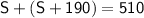
Combine like terms:

`\sf 2S + 190 = 510`

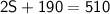
Subtract 190 from both sides:

`\sf 2S + 190 -190 = 510-190`

`\sf 2S = 320`

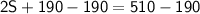
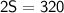
Divide by 2:

`\sf (2S )/(2)=( 320 )/(2)`

`\sf S = 160`

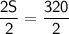
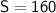
Now that we know the number of acres of squash (
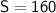`\sf S = 160`), we can find the number of acres of pumpkins using the first equation:

`\sf P = S + 190`

`\sf P = 160 + 190`

`\sf P = 350`

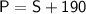
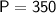
Therefore, Robert's uncle needs to plant 350 acres of pumpkins.