Question

A fairgrounds ride spins its occupants inside a flying saucer-shaped container. If the horizontal circular path the riders follow has a 9.00 m radius, at how many revolutions per minute will the riders be subjected to a centripetal acceleration whose magnitude is 1.80 times that due to gravity

Answer 1

13.37 rev/min

Step-by-step explanation:

acceleration due to gravity (g) = 9.8 m/s², centripetal acceleration (
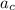`a_c`) = 1.8 * g = 1.8 * 9.8 m/s² = 17.64 m/s².

r = 9 m

Centripetal acceleration (
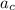`a_c`) is given by:

`a_c=(v^2)/(r) \\\\v=√(a_c*r) \\\\v=√(17.64\ m/s^2*9\ m)\\\\v=12.6\ m/s`

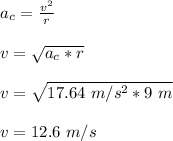
The velocity (v) is given by:

v = ωr; where ω is the angular velocity

Hence:

ω = v/r = 12.6 / 9

ω = 1.4 rad/s

ω = 2πN

N = ω/2π = 1.4 / 2π

N = 0.2228 rev/s

N = 13.37 rev/min