This fraction is not one of the options provided in the multiple-choice answers. Therefore, none of the given options are correct
The image contains an expression that we need to simplify using the properties of exponents, and then evaluate for
 . The expression is:
. The expression is:
![\[ \left( (2a^4)/(a^(0)a^6) \right)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dvrr2l71bmvhif2z2ofh1peadddauvmn89.png)
Let's simplify the expression step by step before substituting the value of
 :
:
1. Simplify inside the parentheses:
-
 (Any non-zero number raised to the 0th power is 1).
(Any non-zero number raised to the 0th power is 1).
-
 divided by
divided by
 due to the quotient rule of exponents
due to the quotient rule of exponents
 .
.
2. The expression inside the parentheses becomes
 .
.
3. Square the result:
-
 is
is
 due to the power of a product rule
due to the power of a product rule
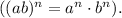
4. Calculate the squared terms:
-
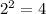
-

5. The simplified expression is
 .
.
Now let's substitute
 into the simplified expression:
into the simplified expression:
![\[ 4(-5)^(-4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7bxg9xnqtcfsq7qsurda562ummaupngvmx.png)
6. Calculate the exponent:
-
 .
.
7. Calculate \( (-5)^4 \):
-
 .
.
8. So,
 .
.
9. Multiply by 4:
-

10. Simplify if possible:
- Since
 cannot be simplified further, this is the final result.
cannot be simplified further, this is the final result.
To find the numeric value:
![\[ 4(-5)^(-4) = 4 \cdot (1)/(625) = (4)/(625) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ki5zpvjghfef5pg7rmguviiq4bu6mcnt5i.png)
This fraction is not one of the options provided in the multiple-choice answers.
the complete Question is given below: