Question

What is the solution set of the quadratic inequality fx) 0?

A X € R
B {x| X=-3)
C. {x] X = 3}
D. w line thru it

Answer 1

The solution set of the quadratic inequality
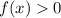`\(f(x) > 0\)` is represented by option A
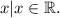`{x | \(x \in \mathbb{R}\)}.` Thus the correct option is A.

Step-by-step explanation:

The solution set of a quadratic inequality can be determined by finding the critical points where the quadratic expression equals zero and then analyzing the sign of the expression in each interval created by these points. In this case, the inequality \(f(x) > 0\) indicates that the solutions lie in the intervals where the quadratic expression is positive.

Considering the options:

- Option A
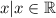`{x | \(x \in \mathbb{R}\)}` represents the set of all real numbers, which is correct for a quadratic inequality where the expression is greater than zero.

- Option B x | (x = -3) represents a specific value and is not suitable for a quadratic inequality with the given condition.

- Option C x | (x = 3) also represents a specific value and is not applicable for the same reason.

- Option D with a line through it typically denotes an empty set, which is not accurate for the given inequality.

Therefore, option A
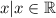`{x | \(x \in \mathbb{R}\)}` is the correct representation of the solution set for the quadratic inequality
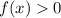`\(f(x) > 0\)` . This indicates that the inequality holds true for all real values of x.