Question

1.32 Factory defective rate. A factory quality control manager decides to investigate the percentage of defective items produced each day. Within a given work week (Monday through Friday) the percentage of defective items produced was 2%, 1.4%, 4%, 3%, 2.2%. (a) Calculate the mean for these data. (b) Calculate the standard deviation for these data, showing each step in detail.

Answer 1

a) the mean percentage of defective item produced is 2.52 %

b) the standard deviation of percentage of defective item produced is 1.01%

Explanation:

Given that;

the percentage of defective items produced was 2%, 1.4%, 4%, 3%, 2.2%.

sample size n = 5

a) Calculate the mean for these data

mean percentage of defective item produced will be;

`x^(bar)` = ∑x / n

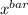`x^(bar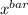)` = ∑x / n = ( 2% + 1.4% + 4% + 3% + 2.2% ) / 5

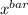`x^(bar)` = 12.6 / 5

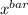`x^(bar)` = 2.52 %

Therefore, the mean percentage of defective item produced is 2.52 %

b) Calculate the standard deviation for these data

Formula for standard deviation is;

S = √( (∑(x-
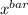`x^(bar)` )²) / (n-1) )

so we make a table;

x ( x -
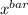`x^(bar)` )% ( x -
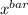`x^(bar)` )²%

2% -0.52 0.2704

1.4% -1.12 1.2544

4% 1.48 2.1904

3% 0.48 0.2304

2.2%. -0.32 0.1024

summation 4.048

so (∑(x-
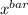`x^(bar)` )² = 4.048%

so we substitute the value into our equation;

S = √( (∑(x-
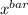`x^(bar)` )²) / (n-1) )

S = √( (4.048%) / (5-1) )

S = √( 4.048% / 4 )

S = √( 1.0121

S = 1.00598 % ≈ 1.01%

Therefore, the standard deviation of percentage of defective item produced is 1.01%