The transformed function is
 obtained by shifting the original function
obtained by shifting the original function
 units downward.
units downward.
The given function is
 . To translate this function 4 units down, we need to subtract 4 from the entire function. The vertical translation of a function
. To translate this function 4 units down, we need to subtract 4 from the entire function. The vertical translation of a function
 downwards by
downwards by
 units is represented as
units is represented as
 .
.
Therefore, the transformed function
 is obtained by subtracting 4 from
is obtained by subtracting 4 from

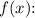
![\[ g(x) = |2x| - 4 \]](https://img.qammunity.org/2024/formulas/mathematics/college/37qra9f756kujxjljv605ou5jmp26y3nx0.png)
This transformation shifts every point on the graph of
 downward by 4 units. The absolute value function
downward by 4 units. The absolute value function
 is symmetric about the y-axis, so the translation affects both the positive and negative regions of the x-axis equally.
is symmetric about the y-axis, so the translation affects both the positive and negative regions of the x-axis equally.
In summary, the equation of the transformed function is
 indicating a vertical translation downward by 4 units compared to the original function
indicating a vertical translation downward by 4 units compared to the original function
 The absolute value function ensures that the graph remains V-shaped, but it is now positioned lower on the coordinate plane.
The absolute value function ensures that the graph remains V-shaped, but it is now positioned lower on the coordinate plane.
Question:
The graph of the function f(x)=|2x| is translated 4 units down. What is the equation of the transformed function?