Question

What is the radial component of the electric field associated with the potential V=ar^-2, where a is a constant?

A. -2ar⁻³
B. -2ar⁻¹
C. ar⁻¹
D. 2ar⁻¹
E. 2ar⁻³

Answer 1

The radial component of the electric field associated with the potential
`\(V = a r^(-2)\) is \(\mathbf{C. \, ar^(-1)}\).`Thus,the correct option is c.

Step-by-step explanation:

To find the radial component
`(\(E_r\))` of the electric field from the potential (V), we can use the relation
`\(E_r = -(dV)/(dr)\).` Given
`\(V = a r^(-2)\)`, we differentiate (V) with respect to (r) to obtain
`\(E_r\)`.

`\[E_r = -(dV)/(dr) = -(d)/(dr)(a r^(-2))\]`

Using the power rule and chain rule in differentiation, we get:

`\[E_r = -(d)/(dr)(a r^(-2)) = 2a r^(-3)\]`

Therefore, the radial component of the electric field is
`\(2a r^(-3)\)`. However, we are asked for the answer in terms of
`\(r^(-1)\)`, so we can rewrite
`\(2a r^(-3)\) as \(\mathbf{ar^(-1)}\).`

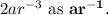
In summary, the radial component of the electric field associated with the given potential
`\(V = a r^(-2)\)` is
`\(\mathbf{ar^(-1)}\)`. This indicates that the electric field decreases as the distance from the source (r) increases, following an inverse relationship with (r).

Therefore,the correct option is c.