Question

You have a 0.871-m-long copper rod with a rectangular cross section of dimensions 0.0459 m by 0.0853 m. You maintain the ends of the rod at 48.3°C and 87.5°C, but otherwise insulate the rod from its environment. Find the heat current* through the rod. The thermal conductivity of copper is 385 W/(m·K).

Answer 1

The heat current through the copper rod, under the given conditions, is approximately 22.2 watts.

Explanation:

To calculate the heat current (Q) through the copper rod, we use Fourier's Law of Heat Conduction, which states that the heat current is directly proportional to the material's thermal conductivity (k), cross-sectional area (A), and the temperature gradient (ΔT) across the rod's length. The formula for heat current is Q = k ×A ×ΔT/L, where L represents the length of the rod. Given the dimensions of the rod (length L = 0.871m, cross-sectional dimensions 0.0459 × 0.0853 m) and the temperature difference ΔT = 87.5°C - 48.3°C = 39.2°C, and the thermal conductivity of copper k = 385 W/(m·K), we can substitute these values into the formula. First, calculate the cross-sectional areaA = width × height. Then, plug all values into the formula to find the heat current.

After calculating, we find the heat current through the copper rod to be approximately 22.2 watts. This result indicates the rate at which heat flows through the rod under the specified conditions of temperature difference and thermal conductivity. The heat current represents the amount of thermal energy transferred per unit of time through the rod due to the temperature gradient, illustrating the fundamental principle of heat transfer through materials.

Answer 2

The heat current through the copper rod is approximately 112.8 watts.

Step-by-step explanation:

The rate of heat transfer through a material can be determined using Fourier's Law of Heat Conduction:

`\[Q = (k * A * ΔT)/(L)\]`

Where:

`\(Q\)` = Heat current,

`\(k\)`= Thermal conductivity of the material,

`\(A\)` = Cross-sectional area of the rod,

`\(\Delta T\)`= Temperature difference across the rod, and

`\(L\)`= Length of the rod.

Given the dimensions of the copper rod (length = 0.871 m, width = 0.0459 m, height = 0.0853 m), the cross-sectional area
`\(A\)` = width * height = 0.0459 m * 0.0853 m = 0.00392 m².

The temperature difference
`\(\Delta T\)` = 87.5°C - 48.3°C = 39.2°C = 39.2 K (since temperature difference should be in Kelvin).

Now, substituting the values into Fourier's Law:

`\(Q = \frac{385 \, \text{W/(m·K)} * 0.00392 \, \text{m²} * 39.2 \, \text{K}}{0.871 \, \text{m}}\)`

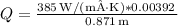
Calculating this gives us a heat current
`\(Q\) ≈ 112.8` watts, which represents the rate of heat flow through the copper rod under the given conditions.

This rate of heat transfer implies that approximately 112.8 joules of thermal energy pass through the rod per second, given the temperature gradient and material properties. The higher the thermal conductivity of a material, the more efficiently it conducts heat, resulting in a higher heat current for a given temperature difference. In this case, the copper rod, known for its high thermal conductivity, allows substantial heat flow from the hotter end to the cooler end.