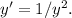Question

verify that y = tan(x c) is a one-parameter family of solutions of the differential equation y' = 1 y2.

Answer 1

In this case, since the square of secant squared is equal to the square of tangent, the equation holds true. Therefore,
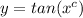`y = tan(x^c)` is indeed a one-parameter family of solutions of the differential equation
`y' = 1/y^2.`

Step-by-step explanation:

To verify that
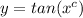`y = tan(x^c)` is a one-parameter family of solutions of the differential equation
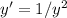`y' = 1/y^2`, we need to substitute
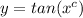`y = tan(x^c)` into the differential equation and show that it satisfies the equation.

1. Start by finding the derivative of y with respect to x:

`y' = d/dx(tan(x^c))`

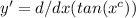
2. Apply the chain rule:

`y' = sec^2(x^c) * d/dx(x^c)`

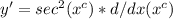
3. Simplify the derivative of
`x^c`:

`y' = c * sec^2(x^c) * (x^c-1)`

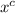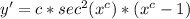
4. Rewrite the expression for y' in terms of y:

`y' = c * (sec^2(x^c)) / (tan^2(x^c))`

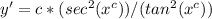
5. Substitute
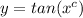`y = tan(x^c)` into the expression for y':

`y' = c * (sec^2(x^c)) / (tan^2(x^c))\\= c * (sec^2(x^c)) / (tan^2(x^c))\\= c * (1/cos^2(x^c)) / (sin^2(x^c)/cos^2(x^c))\\= c / sin^2(x^c)\\= c / (sin(x^c))^2`

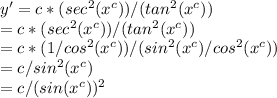
6. Simplify y':

`y' = c / (sin(x^c))^2`

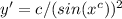
7. Compare y' with the given differential equation
`y' = 1/y^2`:

`c / (sin(x^c))^2 = 1 / y^2`

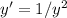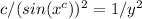
We can see that
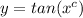`y = tan(x^c)` satisfies the differential equation
`y' = 1/y^2`

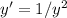
Therefore,
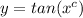`y = tan(x^c)` is a one-parameter family of solutions of the differential equation
`y' = 1/y^2.`