Question

You are one of 2,000 adults. Out of these, 480 still sleep with a stuffed animal, blanket, or other sentimental objects. Construct a 95

Answer 1

Construct a 95% confidence interval for the proportion of adults who still sleep with a stuffed animal, blanket, or other sentimental object:
`\( (0.224, 0.276) \).`

Step-by-step explanation:

To construct a confidence interval for a proportion, you can use the formula:

`\[ \text{Confidence Interval} = \hat{p} \pm Z * \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} \]`

Where:

-
`\( \hat{p} \)` is the sample proportion.

-
`\( Z \)` is the Z-score corresponding to the desired confidence level.

-
`\( n \)` is the sample size.

Given that 480 out of 2,000 adults still sleep with a sentimental object, the sample proportion
`(\( \hat{p} \))` is calculated as
`\( (480)/(2000) = 0.24 \).`

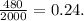
For a 95% confidence interval, the Z-score is approximately 1.96.

Now, substitute these values into the formula:

`\[ \text{Confidence Interval} = 0.24 \pm 1.96 * \sqrt{(0.24 * (1 - 0.24))/(2000)} \]`

Perform the calculations to get the confidence interval:

`\[ \text{Confidence Interval} = (0.224, 0.276) \]`

Therefore, the 95% confidence interval for the proportion of adults who still sleep with a stuffed animal, blanket, or other sentimental object is
`\( (0.224, 0.276) \).`