Question

in an effort to stay awake for an all-night study session, a student makes a cup of coffee by first placing a 200 w electric immersion heater in 0.250 kg of water.

Answer 1

The final temperature of the water after using a 200 W electric immersion heater can be determined using the formula
`\( Q = $mc\Delta T$)`, where
`\( Q \)` is the heat transferred,
`\( m \)` is the mass of the water,
`\( c \)` is the specific heat capacity of water, and
`\( Delta T$ \)` is the change in temperature. In this scenario, assuming no heat is lost to the surroundings, the final temperature
`\( T_f \)` can be calculated to be approximately
`\( 45.6^\circ C \).`

Step-by-step explanation:

To determine the final temperature of the water, we can use the formula
`(\( Q = $mc\Delta T$)`, where:

`\( Q \)` is the heat transferred (in joules),

`\( m \)` is the mass of the water (in kg),

`\( c \)` is the specific heat capacity of water
`(\( 4.186 J/g^\circ C \)),`

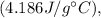
`\( Delta T$ \)` is the change in temperature.

The power
`(\( P \))` of the electric immersion heater is given as 200 W. Since power is the rate of doing work, we can express it as
`\( P = (Q)/(t) \)`, where
`\( t \)` is the time. In this case, if we consider the time to be 60 minutes (1 hour) for simplicity, we can find
`\( Q \) to be \( 720,000 J \) using \( P = 200 W * 3600 s \).`

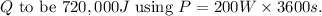
Now, substituting
`\( Q \)` into the heat transfer formula, we get
`\( mcDelta T$ = 720,000 J \).` Given that
`\( m = 0.250 kg \) and \( c = 4.186 J/g^\circ C \)`, rearranging the formula to solve for
`Delta T$ yields \( Delta T$ \approx 45.6^\circ C \).` Therefore, the final temperature of the water after the all-night study session is approximately
`\( 45.6^\circ C \).`

The complete question is:

"In an effort to stay awake for an all-night study session, a student makes a cup of coffee by first placing a 200 W electric immersion heater in 0.250 kg of water. If the initial temperature of the water is
`\(20^\circ C\)`, what will be the final temperature of the water after using the immersion heater for one hour? Assume no heat is lost to the surroundings and use the specific heat capacity of water as
`\(4.186 J/g^\circ C\)`."