Question

15/0
17 km
23.6 km
it says the question needa to be 20 letters long so yea…

Answer 1

The height of the cone is approximately 22 kilometers.

To find the height of the cone, you can use the Pythagorean theorem, as it relates the radius, height, and slant height of a right-angled triangle formed by the cone.

Given the diameter as 17 km, the radius (r) is half of the diameter, so
`\(r = (17)/(2)\) km.`

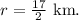
The slant height (I) is provided as 23.6 km.

Apply the Pythagorean theorem:
`\(l^2 = r^2 + h^2\)`, where \(l\) is the slant height, r is the radius, and h is the height.

In this case,
`\(23.6^2 = \left((17)/(2)\right)^2 + h^2\)`.

Solve for h.

Certainly! Let's calculate
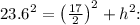
`\(23.6^2 = \left((17)/(2)\right)^2 + h^2\):`

`\[23.6^2 = \left((17)/(2)\right)^2 + h^2\]`

Solving this equation:

`\[h^2 = 23.6^2 - \left((17)/(2)\right)^2\]`

`\[h^2 = 556.96 - (289)/(4)\]`

`\[h^2 = 556.96 - 72.25\]`

`\[h^2 = 484.71\]`

`\[h = √(484.71)\]`

`\[h \approx 22\]`

Therefore, the height of the cone is approximately 22 kilometers.

The probable question may be:

In a cone the diameter of the cone is 17 km and slant height is 23.6 km Find the height of cone.