a.
![\[ y = (x^2 + 6x + 9) - 9 - 1 = (x + 3)^2 - 10 \]](https://img.qammunity.org/2024/formulas/mathematics/college/dg0t0xhtegfw8vl7a065fnjmu2qy8p3in1.png)
b.
![\[ v = (x^2 + 2x + 1) + 6 = (x + 1)^2 + 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/v2giswx0sj3350ulcwyilx2lz032guceke.png)
c.
![\[ y = (x^2 + 10x + 25) - 25 + 20 = (x + 5)^2 - 5 \]](https://img.qammunity.org/2024/formulas/mathematics/college/6gg091s9c47mw8nzduiahujn2vhkq4aeyx.png)
d.
![\[ v = (x^2 + 2x + 1) - 1 = (x + 1)^2 - 1 \]](https://img.qammunity.org/2024/formulas/mathematics/college/eltpz5k7cioejznjvfge55rv9ogqg9m6k3.png)
e.
![\[ y = (x^2 - 6x + 9) - 9 - 4 = (x - 3)^2 - 13 \]](https://img.qammunity.org/2024/formulas/mathematics/college/4zrg2xr4sss5unhd5kaql8e1mbpp4dy5lc.png)
f.
![\[ y = (x^2 - 8x + 16) - 16 - 2 = (x - 4)^2 - 18 \]](https://img.qammunity.org/2024/formulas/mathematics/college/booi7eb7hca45knheqmibbt34alupql2oc.png)
g.
![\[ y = (x^2 - 12x + 36) - 36 + 8 = (x - 6)^2 - 28 \]](https://img.qammunity.org/2024/formulas/mathematics/college/5nwdtp25jxow5ynhk2r82hx4gtz6g1q5ui.png)
To rewrite each given quadratic relation in the form
 by completing the square, we'll follow these steps:
by completing the square, we'll follow these steps:
1. Group the
 and \(x\) terms together.
and \(x\) terms together.
2. Complete the square for the quadratic expression.
3. Rewrite the expression in the desired form.
![a) \(y = x^2 + 6x - 1\):\\ y = (x^2 + 6x + 9) - 9 - 1 = (x + 3)^2 - 10 \]](https://img.qammunity.org/2024/formulas/mathematics/college/9vcu2wj4ra8hl32moe5jzzqa4dcbdsel94.png)
b)

![\[ v = (x^2 + 2x + 1) + 6 = (x + 1)^2 + 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/v2giswx0sj3350ulcwyilx2lz032guceke.png)
c)
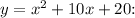
![\[ y = (x^2 + 10x + 25) - 25 + 20 = (x + 5)^2 - 5 \]](https://img.qammunity.org/2024/formulas/mathematics/college/6gg091s9c47mw8nzduiahujn2vhkq4aeyx.png)
d)
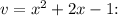
![\[ v = (x^2 + 2x + 1) - 1 = (x + 1)^2 - 1 \]](https://img.qammunity.org/2024/formulas/mathematics/college/eltpz5k7cioejznjvfge55rv9ogqg9m6k3.png)
e)
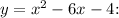
![\[ y = (x^2 - 6x + 9) - 9 - 4 = (x - 3)^2 - 13 \]](https://img.qammunity.org/2024/formulas/mathematics/college/4zrg2xr4sss5unhd5kaql8e1mbpp4dy5lc.png)
f)
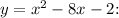
![\[ y = (x^2 - 8x + 16) - 16 - 2 = (x - 4)^2 - 18 \]](https://img.qammunity.org/2024/formulas/mathematics/college/booi7eb7hca45knheqmibbt34alupql2oc.png)
g)
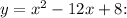
![\[ y = (x^2 - 12x + 36) - 36 + 8 = (x - 6)^2 - 28 \]](https://img.qammunity.org/2024/formulas/mathematics/college/5nwdtp25jxow5ynhk2r82hx4gtz6g1q5ui.png)
In each case, the quadratic relation has been successfully rewritten in the desired form by completing the square.