Question

Tim and Rick both can run at speed vr and walk at speed vw, with

vr>vw. They set off together on a journey of distance D. Rick walks half of the distance and runs the other half. Tim walks half of the time and runs the other half.
How long does it take Rick to cover the distance D?
Express the time taken by Rick in terms of vr, vw, and D.

Answer 1

Rick takes
`\( (D)/(2v_r + v_w) \)` time to cover the distance
`\( D \).`

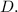
Step-by-step explanation:

To find Rick's total time taken, we consider the time he spends walking and running separately. Let
`\( t_w \)` represent the time Rick spends walking half the distance, which can be calculated as
`\( t_w = (D)/(2v_w) \)` since he walks at speed
`\( v_w \).`

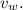
For the running part, Rick covers the other half of the distance at speed
`\( v_r \),` taking
`\( t_r = (D)/(2v_r) \)` time.

The total time taken by Rick is the sum of the time spent walking and running:
`\( t_{\text{total}} = t_w + t_r = (D)/(2v_w) + (D)/(2v_r) \).`

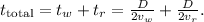
Simplifying this expression, we find a common denominator and add the fractions, resulting in
`\( t_{\text{total}} = (D(v_r + v_w))/(2v_rv_w) \).` Further simplification leads to
`\( t_{\text{total}} = (D)/(2v_r + 2v_w) \).`

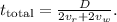
Factoring out the common factor of 2 in the denominator, we get
`\( t_{\text{total}} = (D)/(2v_r + v_w) \),` expressing Rick's total time taken in terms of
`\( v_r \), \( v_w \),` and
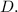`\( D \).` Therefore, Rick takes
`\( (D)/(2v_r + v_w) \)` time to cover the distance
`\( D \),`considering his combination of walking and running speeds.