Question

Which exponential equation correctly rewrites this logarithmic equation? log6 18 = x

1) x18 = 6
2) x6 = 18
3) 6x = 18
4) 18x = 6

Answer 1

The exponential equation that correctly rewrites the logarithmic equation
`\( \log_6 18 = x \)` is
`\( 6^x = 18 \)`.

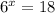The answer is option ⇒3)
`\( 6^x = 18 \)`

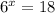
Step-by-step explanation:

To convert the logarithmic equation
`\( \log_6 18 = x \)` to its equivalent exponential form, we can use the definition of a logarithm. The definition states that if
`\( \log_b a = c \)` , then
`\( b^c = a \)`.

In our equation, the base of the logarithm is 6, the logarithmand (the value inside the logarithm) is 18, and the result of the logarithm is
`\( x \)`.

Applying the logarithm definition, we have:

• -
  `\( b = 6 \)` (base of the logarithm)
• -
  `\( a = 18 \)` (logarithmand)
• -
  `\( c = x \)` (result of the logarithm)

Therefore, the equivalent exponential form is:

-
`\( 6^x = 18 \)`

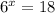
This exponential equation means that if we raise 6 to the power of
`\( x \)`, we will get 18 as the result.

To recap, the correct exponential equation that correctly rewrites the logarithmic equation
`\( \log_6 18 = x \)` is
`\( 6^x = 18 \)`.

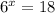The answer is option ⇒3