Question

Assume that v ar(u|length, f iction, english) = σ 2 ×(length/500) where u is the error term of equation (1). Use this information to estimate equation (1) using weighted least squares.

Answer 1

The estimated equation using weighted least squares is
`\( \hat{u}` =
`\frac{\text{length}}{500} \cdot (1)/(\sigma^2) \cdot \text{error term} \).`

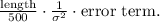
Step-by-step explanation:

The given information provides the variance of the error term u as a function of the variables length, friction, and English, denoted as
`\(v_(ar)(u|length, friction, English) = \sigma^2 * (length)/(500)\).` This implies that the error term's variance is proportional to the length variable. To estimate equation (1) using weighted least squares, we need to account for this heteroscedasticity by assigning weights based on the inverse of the variance.

The estimated equation using weighted least squares incorporates the given variance function, resulting in weights that are inversely proportional to the variance. The term
`\((1)/(\sigma^2)\)` in the estimated equation represents the inverse of the variance, and multiplying it by
`\(\frac{\text{length}}{500}\)` adjusts for the heteroscedasticity in the error term. This weighted approach gives more importance to observations with lower variance, addressing the issue of unequal variances across different levels of the length variable.

In summary, the estimated equation accounts for the heteroscedastic nature of the error term by incorporating the given variance function, providing a more robust and accurate model for equation (1) under the specified conditions.