this question is incomplete, the complete question is:
1. is this model effective
2. what is the correlation coefficient for this data.
3. for a student with a bmi of 25, what is the predicted number of hours under the influence.
Explanation:
1. first of all this model is not effective because we have r² as 0.134. this tells us that only 13.4 percent of the of the variations that exist in this data has been explained by the model
1. we get the correlation coefficient by
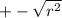
the regression slope coefficient has a negative sign. this is what we would use in calculating the correlation coefficient.
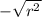
= -√0.134
= -0.366
therefore the correlation coefficient is -0.366
2. to get the number of hours under the influence with a bmi of 25
the equation is
49.2-1.15bmi
= 49.2-1.15(25)
= 49.2-28.75
= 20.45