Question

A cyclist completes q lap around a track in 20s. What is his angular velocity in radians?

Answer 1

The angular velocity of the cyclist is
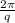`\( (2\pi)/(q) \)`radians per second.

Explanation:

The angular velocity is a measure of how quickly an object rotates or moves in a circular path. In this scenario, the cyclist completes q lap around the track in 20 seconds. Angular velocity is defined as the angle covered in a given time.

For one complete lap, the angle covered is
`\(2\pi\)`radians (a full circle), and as the cyclist completes q laps in 20 seconds, the angular velocity is calculated as
`\( \frac{2\pi \text{ radians}}{q \text{ laps}}`
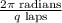
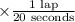`* \frac{1 \text{ lap}}{20 \text{ seconds}} \)`, which simplifies to
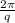`\( (2\pi)/(q) \)` radians per second. This denotes the rate of change of angle per unit of time.

The angular velocity of the cyclist is
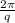`\( (2\pi)/(q) \)`radians per second.