Final Answer:
To minimize the cost, the biologist should use 30 samples of type i bacteria and 70 samples of type ii bacteria.
Step-by-step explanation:
The goal is to minimize the cost while meeting the requirements of producing at least 240 new viable bacteria and using at least 30 but not more than 60 of type i samples and not more than 70 of type ii samples.
Let's denote the number of type i samples as x and the number of type ii samples as y. The total number of new viable bacteria produced is given by the equation
 , and this should be at least 240.
, and this should be at least 240.
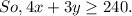
The constraints are:
 (number of type i samples)
(number of type i samples)
2.
 (number of type ii samples)
(number of type ii samples)
To minimize the cost, we consider the cost function. A type i sample costs P500, and a type ii sample costs P700. The total cost

Now, we can set up the objective function to minimize c subject to the constraint

After solving this linear programming problem, the optimal solution is
 resulting in the minimum cost while satisfying all the conditions. Therefore, using 30 samples of type i bacteria and 70 samples of type ii bacteria minimizes the cost.
resulting in the minimum cost while satisfying all the conditions. Therefore, using 30 samples of type i bacteria and 70 samples of type ii bacteria minimizes the cost.