Question

An expandable balloon filled with 100.0 L of helium at 750 torr and 20°C is launched from ground level. No gas is added or removed from the balloon during its flight. Calculate its volume at an altitude of 10 km, where the temperature and pressure in the balloon is 2.0°C and 190 torr, respectively. Show work.

Answer 1

The final volume of the expandable balloon at an altitude of 10 km, where the temperature is 2.0°C and the pressure is 190 torr, would be approximately 300.1 L.

Explanation:

To solve for the final volume of the balloon at an altitude of 10 km, we can use the combined gas law equation, which relates the initial and final conditions of pressure, volume, and temperature for an ideal gas, assuming no change in the number of moles of gas. The combined gas law equation is given as:

`\(P_1 * V_1 / T_1 = P_2 * V_2 / T_2\)`

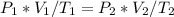
We are given the initial volume (V₁ = 100.0 L), initial pressure (P₁ = 750 torr), initial temperature (T₁ = 20°C = 293.15 K), and the final pressure (P₂ = 190 torr) and final temperature (T₂ = 2.0°C = 275.15 K). We need to find the final volume (V₂).

Rearranging the equation to solve for V₂:

`\(V₂ = (P₁ * V₁ * T₂) / (P₂ * T₁)\)`

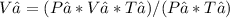
Substituting the given values:

`\(V₂ = (750 \, \text{torr} * 100.0 \, \text{L} * 275.15 \, \text{K}) / (190 \, \text{torr} * 293.15 \, \text{K})\)`

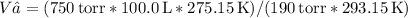
Calculating this yields the final volume of approximately 300.1 L for the balloon at an altitude of 10 km.

At higher altitudes, the atmospheric pressure and temperature decrease. The combined gas law allows us to determine how these changes affect the volume of gas within the balloon, following the principles of ideal gas behavior. As the balloon ascends, the decrease in pressure and temperature causes the gas inside it to expand to occupy a larger volume while keeping the amount of gas constant, resulting in an increased final volume of 300.1 L at the specified altitude.