Question

Required information Skip to question A die (six faces) has the number 1 painted on two of its faces, the number 2 painted on three of its faces, and the number 3 painted on one of its faces. Assume that each face is equally likely to come up. If the die were loaded so that the face with the 3 on it were twice as likely to come up as each of the other five faces, would this change the value of P(odd number)

Answer 1

The change to the face 3 affects the value of P(Odd Number)

Explanation:

Analysing the question one statement at a time.

Before the face with 3 is loaded to be twice likely to come up.

The sample space is:

`S = \{1,1,2,2,2,3\}`

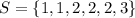
And the probability of each is:

`P(1) = (n(1))/(n(s))`

`P(1) = (2)/(6)`

`P(1) = (1)/(3)`

`P(2) = (n(2))/(n(s))`

`P(2) = (3)/(6)`

`P(2) = (1)/(2)`

`P(3) = (n(3))/(n(s))`

`P(3) = (1)/(6)`

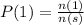
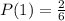
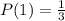
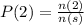
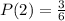
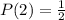
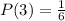
P(Odd Number) is then calculated as:

`P(Odd\ Number) = P(1) + P(3)`

`P(Odd\ Number) = (1)/(3) + (1)/(6)`

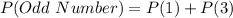
Take LCM

`P(Odd\ Number) = (2+1)/(6)`

`P(Odd\ Number) = (3)/(6)`

`P(Odd\ Number) = (1)/(2)`

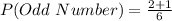
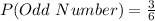
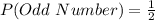
After the face with 3 is loaded to be twice likely to come up.

The sample space becomes:

`S = \{1,1,2,2,2,3,3\}`

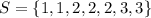
The probability of each is:

`P(1) = (n(1))/(n(s))`

`P(1) = (2)/(7)`

`P(2) = (n(2))/(n(s))`

`P(2) = (3)/(7)`

`P(3) = (n(3))/(n(s))`

`P(3) = (1)/(7)`

`P(Odd\ Number) = P(1) + P(3)`

`P(Odd\ Number) = (2)/(7) + (1)/(7)`

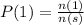
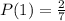
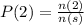
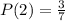
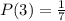
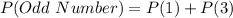
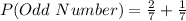
Take LCM

`P(Odd\ Number) = (2+1)/(7)`

`P(Odd\ Number) = (3)/(7)`

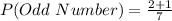
Comparing P(Odd Number) before and after

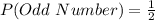`P(Odd\ Number) = (1)/(2)` --- Before

`P(Odd\ Number) = (3)/(7)` --- After

We can conclude that the change to the face 3 affects the value of P(Odd Number)