Final Answer:
The arc length formula and the given information to find θ. s = 4 m, r = 13 m; θ =
![\[ \theta = 4 \, \text{rad} \]](https://img.qammunity.org/2024/formulas/physics/high-school/mf5gx1dqqf7d60g8aum81pfbk2rqa6izhq.png)
Step-by-step explanation:
The arc length formula is given by
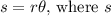 is the arc length,
is the arc length,
 is the central angle in radians. In this case,
is the central angle in radians. In this case,
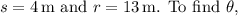 rearrange the formula to solve for
rearrange the formula to solve for
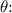
![\[ \theta = (s)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/tvc6bya72gckf47vw8orz2z7yqjebb6oc2.png)
Substitute the given values:
![\[ \theta = \frac{4 \, \text{m}}{13 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ash3pyh1x3gqkrb5745xowh1przgxj86mt.png)
Simplify the fraction:
![\[ \theta = (4)/(13) \, \text{rad} \]](https://img.qammunity.org/2024/formulas/physics/high-school/uax05rji8lgiqipjevymzkhns5km8e8vh5.png)
Thus, the correct answer is
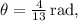 which corresponds to the option "four divided by thirteen rad" in the choices provided.
which corresponds to the option "four divided by thirteen rad" in the choices provided.
This result makes sense intuitively – the angle is a fraction of the full circle, indicating that the arc length of 4 meters is a small portion of the circumference of a circle with a radius of 13 meters. The answer is consistent with the mathematical relationship between arc length, radius, and central angle in a circle.