Question

Use synthetic division to find all the factors of this polynomial: 4x³ + 5x² - 18x + 9?

Answer 1

To find the factors of the polynomial 4x³ + 5x² - 18x + 9, you can use synthetic division.

Step-by-step explanation:

The polynomial 4x³ + 5x² - 18x + 9 can be factored using synthetic division to find its factors.

Set up the synthetic division table with the coefficients of the polynomial: 4, 5, -18, 9.

Find a factor of the polynomial. This can be done by testing some possible factors and checking if they produce a remainder of 0 when substituted into the polynomial.

Perform synthetic division using the chosen factor and divide the polynomial by it.

If the remainder is 0, the chosen factor is a factor of the polynomial and the result of the division will give a new polynomial of lower degree.

Repeat the process with the new polynomial until it cannot be factored further.

The factors of the polynomial are the results obtained from the divisions.

Answer 2

the factors of the polynomial
`\( 4x^3 + 5x^2 - 18x + 9 \)` are:

`\[ (x - 3)(4x^2 + 17x + 33) \]`

And
`\( 4x^2 + 17x + 33 \)` does not factor further over the reals.

To find the factors of the polynomial
`\( 4x^3 + 5x^2 - 18x + 9 \)` using synthetic division, we need to identify possible rational roots using the Rational Root Theorem. The possible rational roots are the divisors of the constant term divided by the divisors of the leading coefficient.

The divisors of the constant term (9) are
`\( \pm1, \pm3, \pm9 \)`.

The divisors of the leading coefficient (4) are
`\( \pm1, \pm2, \pm4 \)`.

The possible rational roots are
`\( \pm1, \pm3, \pm9, \pm(1)/(2)`,
`\pm(3)/(2), \pm(9)/(2) \)`.

We will test these possible roots using synthetic division until we find a factor. If the remainder is 0, we have found a factor.

Let's start with
`\( x = 1 \)`:

```

_________________________

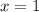1 | 4 5 -18 9

| 4 9 -9

|______________________

4 9 -9 0

```

Since the remainder is not 0,
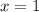`\( x = 1 \)` is not a root. We continue testing the possible roots. Let's try
`\( x = -1 \)`:

```

_________________________

-1 | 4 5 -18 9

| -4 1 17

|______________________

4 1 -17 26

```

Again, the remainder is not 0, so
`\( x = -1 \)` is not a root. We proceed with the next possible rational root, which is
`\( x = 3 \)`:

```

_________________________

3 | 4 5 -18 9

| 12 51

|______________________

4 17 33 0

```

Here we have a remainder of 0, which means
`\( x = 3 \)` is a root of the polynomial.

Now the polynomial can be written as:

`\[ (x - 3)(4x^2 + 17x + 33) \]`

To find the remaining factors of
`\( 4x^2 + 17x + 33 \)`, we would look for roots of this quadratic, which we can find using the quadratic formula, factoring, or completing the square. However, a quick check of the discriminant,
`\( b^2 - 4ac = 17^2 - 4 \cdot 4 \cdot 33 \)`, shows that it is negative:

`\[ 289 - 528 = -239 \]`

Since the discriminant is negative, the quadratic has no real roots and thus cannot be factored further over the real numbers.

Therefore, the factors of the polynomial
`\( 4x^3 + 5x^2 - 18x + 9 \)` are:

`\[ (x - 3)(4x^2 + 17x + 33) \]`

And
`\( 4x^2 + 17x + 33 \)` does not factor further over the reals.