Question

10.A noted psychic was tested for ESP. The psychic was presented with 200 cards face down and askedto determine if the card was one of five symbols: a star, cross, circle, square, or three wavy lines. Thepsychic was correct in 50 cases. To determine if he has ESP, we want to know if his success rate is betterthan someone who just guesses. That is, we test the hypotheses H0: p

Answer 1

Explanation:

The sample proportion
`\hat p = (50)/(200)`

`\hat p = 0.25`

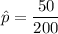
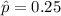
The null hypothesis and the alternative hypothesis:

`H_o: p = 0.20 \\ \\ H_1 : p > 0.20`

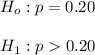
Thus; the test statistics is:

`Z = (\hat p - p_o)/((p_o(1-p_o))/(n) )`

`Z = \frac{0.25 -0.20}{\sqrt{(0.20(1-0.20))/(200) }}`

`Z = \frac{0.05}{\sqrt{(0.16)/(200) }}`

`Z = (0.05)/(√(0.0008 ))`

`Z = 1.768`

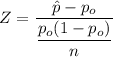
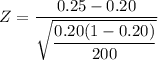
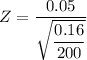
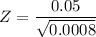
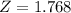
P-value = 2 × P(Z< - 1.768)

From the z tables

P-value = 2 × 0.03853

P-value = 0.07706

Thus, the p-value is 0.05 < P-value < 0.10