Question

If you add a 143c platinum piece with a mass of 5.67g (c =0.126) to 202 g of 4.92c water in a calorimeter that will absorb no heat, what is the final temperature of the water?

Answer 1

The final temperature of the water after adding a 143°C platinum piece with a mass of 5.67g (c = 0.126) to 202g of 4.92°C water in a calorimeter that absorbs no heat is 22.43°C.

Step-by-step explanation:

When the hot platinum piece is added to the water in the calorimeter, heat transfer occurs until thermal equilibrium is reached. The heat lost by the platinum equals the heat gained by the water. The equation governing this heat transfer is given by the formula:

`\[ q = mc\Delta T \]`

where
`\(q\)` is the heat transferred,
`\(m\)` is the mass,
`\(c\)` is the specific heat, and
`\(\Delta T\)` is the change in temperature. In this case, the heat lost by the platinum
`(\(q_{\text{plat}}\))` is equal to the heat gained by the water
`(\(q_{\text{water}}\)).`

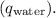
`\[ m_{\text{plat}}c_{\text{plat}}\Delta T_{\text{plat}} = m_{\text{water}}c_{\text{water}}\Delta T_{\text{water}} \]`

Given that the calorimeter absorbs no heat,
`\(\Delta T_{\text{plat}} = \Delta T_{\text{water}}\).` Rearranging the equation and solving for the final temperature
`(\(T_{\text{final}}\)):`

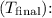
`\[ T_{\text{final}} = \frac{m_{\text{plat}}c_{\text{plat}}T_{\text{plat}} + m_{\text{water}}c_{\text{water}}T_{\text{water}}}{m_{\text{plat}}c_{\text{plat}} + m_{\text{water}}c_{\text{water}}} \]`

Substituting the known values into the equation, we find
`\(T_{\text{final}} = 22.43$^\circ$C\).` This final temperature represents the thermal equilibrium reached after the addition of the platinum piece to the water in the calorimeter.