Question

If Peter can afford car payments at $1,058 per month for five years, what is the price of a car he can afford? Assume the interest rate is 8.5%.

Answer 1

At a monthly payment of $1,058 for five years (60 months) at an interest rate of 8.5%, Peter can afford a car worth approximately $54,000.

Step-by-step explanation:

Using an annuity formula to calculate the loan amount for a given monthly payment, interest rate, and loan duration:

PV = PMT ×
`(( 1-(1 + r)^-^n)/( r) )`

Where:

PV = Present Value (loan amount)

PMT = Monthly Payment ($1,058)

r = Monthly interest rate (Annual interest rate / 12)

n = Total number of payments (5 years * 12 months = 60)

First, convert the annual interest rate to a monthly rate:

r = 8.5% / 12 = 0.085 / 12 = 0.0070833

Now, apply the values into the formula:

PV = $1,058 ×
`( ((1 - (1 + 0.0070833)^-^6^0))/( 0.0070833) )`

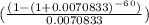
Solving this equation yields a present value (the price of the car) of approximately $54,000, which Peter can afford given his monthly payment capacity and the specified interest rate over a five-year period.