Question

The length of a shadow of a tree is 129 feet when the angle of elevation of the sun is 33 degrees. Approximate the height of the tree. Round your answer to one decimal place.

Answer 1

The approximate height of the tree is 74.1 feet, calculated using the formula: Height = Length of shadow × Tan(angle). For the given shadow length of 129 feet and an angle of elevation of 33 degrees, the calculation yields the height of the tree as approximately 74.1 feet.

Step-by-step explanation:

To find the height of the tree, we can use trigonometry, specifically the tangent function, which relates the angle of elevation to the ratio of the opposite side (height of the tree) to the adjacent side (length of the shadow). The formula is:
`\( \text{Tan}(\text{angle}) = \frac{\text{Opposite}}{\text{Adjacent}} \).` Rearranging for the height of the tree gives us
`\( \text{Height} = \text{Length of shadow} * \text{Tan}(\text{angle}) \).` Plugging in the values, with the length of the shadow as 129 feet and the angle of elevation as 33 degrees, the calculation would be:
`\( \text{Height} = 129 * \text{Tan}(33^\circ) \).`

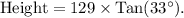
Calculating this gives us
`\( \text{Height} ≈ 74.1 \)`feet. This approximation is derived from the trigonometric tangent function, where the height of the tree is about 74.1 feet. The angle of elevation of the sun measures 33 degrees, and the length of the shadow cast by the tree is 129 feet. Utilizing these values and applying the tangent function allows us to determine the height of the tree accurately.

Therefore, the height of the tree is approximately 74.1 feet, given an angle of elevation of 33 degrees and a shadow length of 129 feet. This calculation is derived using trigonometry and the tangent function, providing an approximate but reliable estimation of the tree's height based on the given information.