Answer:
Explanation:
From the given information:
Assume X represents the no. interviewed until 1 has advanced training.
X obeys a Geometric distribution with parameter 0.3.
X
 Geom (0.30)
Geom (0.30)
For geometric distribution, the probability density is:
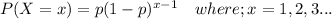
TO calculate the required probability;
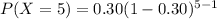
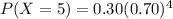
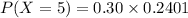
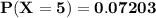
(b)
The expected no. of applicants that need to be interviewed are:

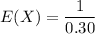
E(X) = 3.33
(c)
The mean and the variance can be computed as:
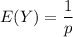
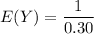
E(Y) = 3.33
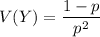

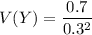
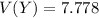
Suppose C represents the no. of the total cost and given that each interview costs $30.
Then C = 30Y
Recall that; C is constant for a random variable X
∴
E(C) = E(30Y)
E(C) = 30E(Y)
E(C) = 30*3.33
E(C) =99.9
E(C)
 100
100
V(C) = V(30Y)
V(C) = 900 V(Y)
V(C) = 900*7.778
V(C) = 7000.2
V(C)
 7000
7000